LFPs | MATLAB Workshop

Human Subjects Making Hand Gestures: Local Field Potential Data

This open-source dataset from Miller 2019 (full database here) includes electrocorticography (ECoG) data recorded from human subjects while they were asked to pinch their fingers or relax. ECoG electrodes are placed right on the surface of the brain, under the dura, and pick up local field potentials (LFPs), which represents population-level activity rather than a single neuron's firing. A lot of LFP analysis is based on extracting salient brain waves (or neural oscillations) from the noisy signal and trying to interpret that. We know that high gamma frequencies (~70-120 Hz) increase in the motor cortex during movement relative to rest (see figure below). We're going to try to replicate that finding using this dataset.

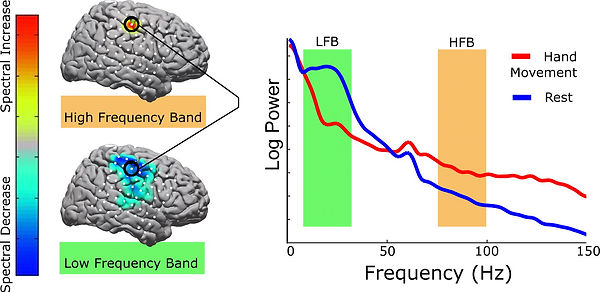
This is probably the most complicated project, so take it slow and make sure you keep track of what you do! Also full disclosure I work with ECoG data so excuse any pro-ECoG biases below...

MATLAB Concepts Covered:

using available data to delineate between trials, epoching, using multidimensional matrices, using other people's code, filtering

Beginner Project: Clean up the data and compare gamma band power during and after a gesture.

1. Load in the data and examine the variables.

Load in the file called wm.mat. There will be four variables: data, dg, srate, and stim.

data: this variable holds all of the electrocorticographic data, with each row representing a time point at which a sample was taken and each column representing a single electrode. Open wm_electrodelocs.fig to see where these electrodes are on the brain (the electrodes here will correspond to #1-64 in the figure).

dg: this variable holds data on the movement of the 5 digits of the subject's hand over the same time course as the ECoG data. You won't need it for this project.

fs: the sampling rate in Hz (samples/second) for the other three variables.

Would a recording sampled at this rate be able to pick up 1000 Hz oscillations? (click for answer)

No.

stim: records when there was a prompt on the screen indicating that the subject should move (nonzero values) and when there was no prompt on the screen (zeros).

How many unique values are there in stim? (click for answer)

2 (0 = no stim, 1 = pinch)

2. Get to know the data.

How long, in seconds, was the experiment? (click for answer)

130.04 sec

At what sample number was the subject first told to move? (click for answer)

7081

Click for hint.

Look for the first nonzero value in stim.

Potentially helpful Google keywords: find

How many seconds of the experiment, total, was the stimulus on? (click for answer)

60 sec

How many individual stimuli were presented? There are a number of ways to calculate this but there isn't (as far as I know!) one simple function to do that for you. While you could just plot stim and count the peaks, I'd encourage you not to do that. (click for answer)

30 stimuli

Click for hint.

My solution relies heavily on a differential. What do the first time points of each stimulation have in common that the other time points don't have?

Potentially helpful Google keywords: find, difference

How much time, in seconds, is there between stimulus presentations?

2 seconds

3. Make a list of information you will need from your data.

Your ultimate goal is to compare the high gamma power of an electrode in the motor cortex during and after stimulus presentation. We'll need the during stimulus and after stimulus data to be epoched (split into trials) before we can start cleaning it up and performing analyses. What information do you need to extract?

Click for the full list of information that I came up with (not exhaustive - you may find other things useful!)

start indices of stimulus presentations
end indices during stimulus presentations
epoched ECoG data for periods during stimulus presentation
epoched ECoG data for periods after stimulus presentation

4. Calculate each piece of information and put it in a variable.

I feel like epoching is kind of a mixture between a logic puzzle and efficiency maximization. It can be a bit frustrating, but it is very helpful for learning the ropes in MATLAB so I'm making you do it!

start and end indices of each stimulus presentation

* if you used differentials in part 2, you already have part of this done. For those who didn't use differentials, remember the fact that there will be a large gap between separate stimuli that won't be present within individual stimuli. If you're able to find the indices of those big jumps, you'll have some of the information.

Click for hint.

You'll need the functions find(), abs(), and diff(), as well as a >/</==. If you're really stuck, click for my solution and keep on moving, but come back to make sure that you understand how this worked!

allstims = find(stim); % this gives us every index at which stim is nonzero (i.e. the

% stimulus is on)

allstims_diff = abs(diff(allstims) % this gives us the absolute difference between these

% indices, which will either be 1 (for two points in

% the same stimulus) or a large number (for two points

% in different stimuli)

gaps= find(allstims_diff > 1); % this is the index of that big jump in allstims_diff

idx = allstims(gaps); % but you need to go back to allstims to get an index that matches

% the stim variable

%% this could be written more concisely (but more confusingly) as:

allstims = find(stim);

idx = allstims(find(abs(diff(allstims)) > 1));

Are these indices the start or end of the stimulus? (click for answer)

the ends

Click for hint.

Try plotting the stim variable overlayed with dots at the indices you've found. Because plotting is annoying and not the main point here, here's how you would do that:

plot(stim);

hold on

plot(idx, 1, 'or') % this will plot a red circle at y = 1 at all the points in idx

* now that you have indices for one end of the stimulus, the other end should be easy! We're going to take it as given that each stimulus is the same length, and you can find this easily with information you already have from part 2.

the epoched ECoG data from each stimulus and rest interval

* first, we're going to need to best store this information. I think the easiest way to store it is as 2 separate 3-dimensional matrices: one for during stimulus and one for during rest. The first dimension is time and the second dimension is channels, like the data variable, but now we'll put trials on the third dimension.

How long will the first dimension of these variables be? (click for answer)

2000 samples (2 sec)

* now we'll need to fill these arrays using a for loop and the start and stop indices you've already

found. The iterating variable of the for loop will the the third dimension (trials). Your code

should follow this general format:

% initialize variables

for iter = 1:numTrials

% pull data from between starts and stops for during stimulus

% pull data from between stops and the next start for after stimulus

end

There are few tricks here: you don't want any overlap between the two conditions, you want them both to be the same length, and you're going to have to do something special for the last trial (your first loop might give you an error - try to figure out why!).

5. Make the data usable, extract high gamma, and plot what you find.

First, we need to clean up the data to make it more usable. (Try plotting one of the trials as it is now to see why it is not super illuminating at the moment).

* step one here is to remove any channels that are obviously nonsense (they were off the surface of the brain, or they were really noisy for some reason). Take a look at the plot to see if there are any suspicious channels (they have significantly different amplitudes than other channels, they seem to only be oscillating at one frequency, something crazy or spiky happens in the middle, obvious things). Spoiler alert: there is one bad channel. Plot all channels in the first trial to see which one.

Which channel is bad? (click for answer)

channel 34

* next, we're going to take out any noise that all of the channels have in common. Open the function commonAverageReference() (in the LFP folder). This is a pared down version of code that's been in my lab for maybe 10 years and has no comments, which also probably 95% of the code you'll be given in real life. Figure out how to use it and what it does!

What variables should you give it, and in what order? (click for answer)

neural data, then the bad channel index

When you give this function the epoched data, it throws an error. Why? (click for answer)

it can't handle 3D arrays

We want to apply this function to the epoched data. Try to get around this error.

Click for hint.

Try using a for loop to iterate through the third dimension.

What does this function do? It uses some fancy matrix multiplication, so don't worry if it isn't immediately obvious. (click for answer)

it subtracts the average of all channels at a given time point from each value

* one last cleaning step! When you do electrophysiology in a hospital environment, for example, you're going to pick up a lot of noise in addition to the signal. We've hopefully removed a lot of this with the common average reference, but there is likely a lot of powerline noise still in there from all of the electronics, lights, etc. in the environment. In the US, powerline noise is at 60 Hz, so we're going to remove frequencies around 60 Hz, 120 Hz, and 180 Hz (multiples of the frequency will have resonance and also add noise). We'll use a notch filter to remove these frequencies. I've given you a function called "notch" to do this. Don't worry about the details of filter design, but do check the top plot that it spits out to make sure it is removing the frequencies you are asking it to.

What variables should you give it, and in what order? (click for answer)

data, frequency to remove, sampling rate

Does this work on the epoched data? (click for answer)

yes! So give it the epoched data

How many frequencies are actually removed by notch()? (click for answer)

7: freq +/- 3

Click for hint.

Look at the second argument given to the function butter(). Look at the butter() documentation if you need to.

Now we're going to extract the power at high gamma frequencies (70-120 Hz), which are associated with movement.

* There's a lot of complicated time-frequency stuff folded into this that will be covered in Neuro 545, so for now just take me at my word and use the function extractHighGammaPower() on the epoched data. Another filter is involved, look at the plot this spits out and compare to the notch filters from before. This one only allows frequencies in the high gamma range through.

* filters sometimes do funky things to the edges of time series. Now that we're done filtering, let's grab one second from the middle of each condition at take out a half second on each end.

How do you get rid of those time periods? (click for answer)

data_small = data_epoched(fs/2:(3*fs/2) - 1, :, :)

* this matrix should be the exact same size as the one we started with. If you plot it, you'll see that it looks a little nicer than before, but what we really want is to get one value per channel. To do this, average over all trials, then over all time points.

Click for hint.

You can give mean() two arguments instead of one, with the second argument defining which dimension to take the mean along.

What size matrix do you end up with? (click for answer)

1 by 64 (one value per channel)

We started with one monster matrix and now we have two small matrices. All that's left is to plot it. We'd like to compare the "on" and "off" conditions for each channel, so let's make a bar chart. Look at the bar() documentation to determine how to get the chart to appear with pairs of bars for each channel.

6. This was a doozy so I'm not going to make you iterate or apply this to another dataset (although there is another patient worth of data in the folder if you want to do that on your own!). Instead, let's take a sec to interpret the bar plot we got.

Obviously, we haven't done any stats here (something else you could do on your own if you want!), but on my plot there are three channels that stand out as having a big high gamma power difference between on and off conditions. Locate any electrodes that look interesting to you on wm_electrodelocs.fig. Try to figure out what general anatomical regions these electrodes are in an interpret these findings.

Click for my results and interpretation.

To me, it looks like electrodes 19, 28, 29, and 36 have higher average high gamma power in the stimulus on condition versus the stimulus off condition. I'd estimate that 19, 28, and 29 are in the primary motor cortex and 36 is in the primary somatosensory cortex. We know that high gamma in the motor cortex increases during movement, so that makes sense (especially electrode 19, which looks like it might be in the hand area of the motor cortex, which makes sense because during the stimulus presentation the subject was asked to move their hand). I'm not sure what to make of the sensory electrode with higher gamma - I'd have to do some lit searching and asking around which I'm not going to do right now but again, you're welcome to. It is somewhat surprising that more electrodes in the motor cortex didn't show this high gamma bump, but we did a lot of averaging so maybe some of it got obscured. Also, we grabbed a second in the middle of the period when the stimulus was on and the period when the stimulus was off, but those don't necessarily correlate to periods when the subject was actually moving, it was just when they were being told to move.

Advanced Project Ideas

There are more or less infinite things you can do with LFP data - the squiggly lines aren't going to interpret themselves! Definitely identify bad channels, common average reference, and notch out powerline noise as described above, but here are some other ideas of things you could do:

Instead of epoching using the stim variable, use the dg variable to find periods when the subject was moving their thumb and/or forefinger a lot versus periods where they weren't moving so much. Compare high gamma during move/non-move conditions.
Look at the time course of high gamma in motor channels (i.e. 19) over the entire experiment. See if there are any correlations between high gamma increases and movements, as seen in the dg variable. You could even play with the corr() and xcorr() functions to try to get numbers to describe this.
Play around with the functions pwelch() and spectrogram() to look at what's going on over a broader range of frequencies. Are there any others that stand out particularly?